Evaluating India’s Strategic Partnerships using Analytic Hierarchy Process
Introduction
A strategic partnership is a long-term interaction between two countries based on political, economic, social and historical factors. Such a partnership manifests itself in a variety of relationships. India has signed “strategic partnerships” with more than 30 countries. Are these countries equally important for India? Or do they have their own hierarchy? For instance, India has strategic partnerships with the United States, Russia, China, Japan, UK, France and others. It is obvious that not all strategic partnerships are equally important. Some have a dominant political element, while others have a prominent economic dimension. In some cases, the security dimension may be the most important. Is there a way to rank the partnerships on the basis of multiple criteria? Which strategic partnership is more important than others?
This work has been inspired by the need to devise a more effective method based on expert judgments using statistical techniques to rank the preferences. We look at India’s relationship with the United States, Russia, Japan, UK and China, on the basis of five parameters, namely economics, politics, defence, technology and people-to-people and rank them in order of importance.
Analytic Hierarchy Process
Analytic Hierarchy Process (AHP)1 is one of the multi-criteria decision making methods based on relative priorities assigned to each criterion in achieving the stated objective. This technique (which to the best of our knowledge has not been previously used for analyzing strategic partnerships) exploits the powerful idea of evaluation and selection of options based on a consistency test, which goes with the subjective judgment of experts. Furthermore, the actual process of carrying out the analysis helps the decision maker to prioritize the parameters in a manner that otherwise might not be possible.
1 Thomas L. Saaty (1990), “How to make a decision: The Analytic Hierarchy Process”, European Journal of Operational Research, 48, 9-26 9 North-Holland, http://www.elsevier.com/authored_subject_sections/S03/Anniversary/EJOR_f….
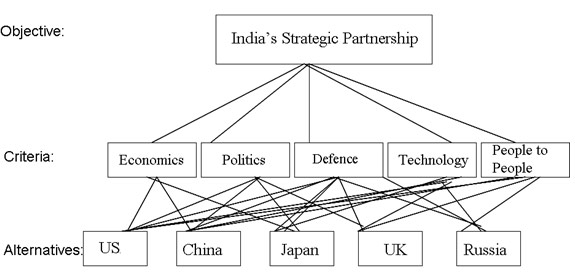
The AHP ranking model relies on subjective assessments of various experts. To begin with, an objective for a decision is stated (in this case, the importance of India’s strategic partnership with a particular country); a set of relevant criteria is chosen and a set of alternatives (i.e. US, UK, Japan, etc.) are expressed. The overall goal of the decision is presented at the top level of hierarchy as depicted in Figure 1. The second level represents the main criteria that define India’s strategic partnerships. Finally, at the lowest level of the hierarchy are the partner countries, which are the decision options as shown in Figure1.
Figure 1: A hierarchy model for the selection of India’s strategic partnership
Methodology
Firstly, a pair-wise comparison of selected criteria is performed. We assess India’s strategic partnerships in terms of five criteria namely: economics, politics, defence, technology and people-to-people factors. Pair-wise comparison begins with comparing the relative importance of two selected criteria. Assuming n attributes, the pair-wise comparison of attribute i with attribute j yields a square matrix where aij denotes the comparative importance of attribute i with respect to attribute j. In the matrix, aij = 1 when i = j and aij=1/aji. An attribute compared with itself is assigned the value 1, so the main diagonal entries of the pair-wise comparison matrix are all 1. Therefore, there are
n x (n-1) judgments required to fill in a n x n matrix. The judgments are entered using the fundamental scale of the AHP (Table 1). The numbers 3, 5, 7 and 9 correspond to the judgments “moderate importance”, “strong importance”, “very strong importance”, and “absolute importance” (with 2, 4, 6, and 8 for compromise between these values). Hence, the relative importance of India’s relationship with other countries based on different criteria under study is evaluated using the opinion of 15 experts. Similarly, the relative importance of India’s relation with country A vis-à-vis country B with reference to different criteria under study is evaluated.
| Intensity of importance | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | Two factors contribute equally to the objective |
| 3 | Moderate importance of one over another | Experience and judgment slightly favour one over the other |
| 5 | Essential or strong importance | Experience and judgment strongly favour one over the other |
| 7 | Very strong importance | Experience and judgment very strongly favour one over the other. Its importance is demonstrated in practice |
| 9 | Extreme importance | The evidence favouring one over the other is of the highest possible validity |
| 2,4,6,8 | Intermediate values | When compromise is needed |
Since the comparisons of factors are done through the subjective judgment of experts, some degree of inconsistency is expected to occur. To avoid that, each matrix of pair-wise comparisons of the criteria is subjected to mathematical verification called ‘consistency ratio (CR)’. CR is the ratio of consistency index (CI) to random index (RI) defined as
where the consistency index is defined as
Where n is the matrix size and is the maximum eigen value. The random index (RI) is often chosen from a pre-calculated Table 2. Hence, using Equation 1, the consistency ratio of each judgment is calculated. If CR0.10 serious inconsistencies may exist and the AHP may not yield meaningful results.
Table 2: The Random consistency index
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
Lastly, the priority vector of each criterion in relation to different countries is calculated. For example, the vectors of priorities are defined as
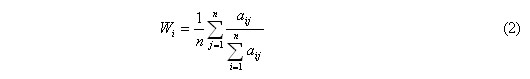
The vectors of priorities are the principal eigenvectors of the matrix aij. It gives the relative priority of the criteria measured on a ratio scale.
Results and Discussion
After the priority vectors for each criterion in relation to different countries are calculated, the last step is to establish the overall priorities of the criteria. We lay out the priorities of each criterion in relation to India’s partnerships with other countries and multiply each column of vectors by the priority of the corresponding criteria and add across each row which results in the desired vector of India’s strategic partnership. Table 3 shows our final results.
| Ranking | India’s strategic Partner’s | Priority Vectors |
|---|---|---|
| 1 | US | 0.4084 |
| 2 | Russia | 0.2412 |
| 3 | China | 0.1627 |
| 4 | Japan | 0.1561 |
| 5 | UK | 0.1451 |
Thus, in the opinion of fifteen experts polled, the Indo-US partnership is the most important with a score of 0.4084, followed by the partnerships with Russia, China, Japan, and UK. In Table 4, the comparisons of India’s partner countries with respect to the criteria and their priorities are listed. For instance, Table 4 (first column) shows that the priority, economic dimension, is strongest in the case of the Indo-Japan partnership. In the case of the Indo-US partnership, the political parameter is predominant. Defence cooperation takes precedence over all other aspects in the Indo-Russia partnership. The Indo-UK partnership is dominated by people-to-people considerations. And in Sino-India relations, the political parameter is the key.
| Economics | Politics | Defence | Technology | People-to-People | |
| India & US | 0.1433 | 0.5046 | 0.0756 | 0.0435 | 0.2330 |
| India & Russia | 0.796 | 0.2121 | 0.4903 | 0.1814 | 0.0367 |
| India & Japan | 0.5097 | 0.2602 | 0.0364 | 0.1055 | 0.0881 |
| India & UK | 0.1617 | 0.4450 | 0.0522 | 0.0522 | 0.2890 |
| India & China | 0.3446 | 0.4518 | 0.0784 | 0.0320 | 0.0933 |
The AHP technique as demonstrated above helps prioritize India’s strategic partnership. In principle, the exercise can be further expanded by including more countries, more parameters and more experts.







